ANSWER:
19.
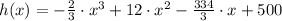
20. 120 m
Explanation:
Let h(x) denote height at any bounce x:
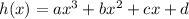
When x = 0
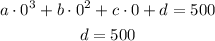
When x = 1
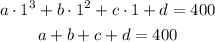
When x = 2

When x = 3
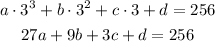
Now, we calculate 3 equations by subtracting the value of d, in order to calculate the value of a, b and c, like this:
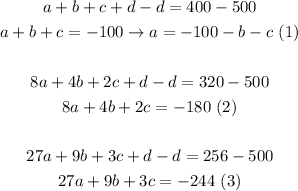
We solve the system of equations as follows:
Replacing (1) in (2) and (3):
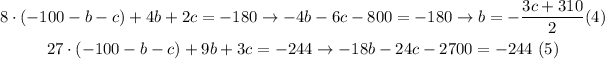
Replacing (4) in (5) and solving for c:
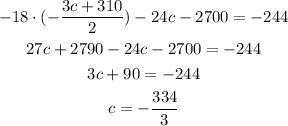
We replace the value of c in (4):
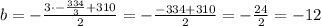
Now we replace the values of b and c in (1):
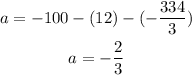
Therefore, the a rule to represent the height of then ball after each bounce is the following:
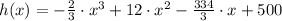
The height after the sixth bounce , would be when x = 6, we replace:

The height after the sixth bounce is 120 meters