Question

i’m studying geometric sequences and i have a question that i’m very stuck on. it says: “a ball is dropped from a height of 500 meters. the table shows the height of each bounce.” “bounce:height (m)”1. 4002. 3203. 256“write a rule to represent the height of then ball after each bounce”“how high does the ball bounce on the 6th bounce?”

Answer 1

19.

`h(x)=-(2)/(3)\cdot x^3+12\cdot x^2-(334)/(3)\cdot x+500`

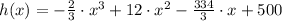
20. 120 m

Explanation:

Let h(x) denote height at any bounce x:

`h(x)=ax^3+bx^2+cx+d`

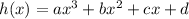
When x = 0

`\begin{gathered} a\cdot0^3+b\cdot0^2+c\cdot0+d=500 \\ d=500 \end{gathered}`

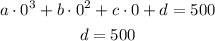
When x = 1

`\begin{gathered} a\cdot1^3+b\cdot1^2+c\cdot1+d=400 \\ a+b+c+d=400 \end{gathered}`

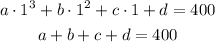
When x = 2

`\begin{gathered} a\cdot2^3+b\cdot2^2+c\cdot2+d=320 \\ 8a+4b+2c+d=320 \end{gathered}`

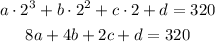
When x = 3

`\begin{gathered} a\cdot3^3+b\cdot3^2+c\cdot3+d=256 \\ 27a+9b+3c+d=256 \end{gathered}`

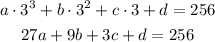
Now, we calculate 3 equations by subtracting the value of d, in order to calculate the value of a, b and c, like this:

`\begin{gathered} a+b+c+d-d=400-500 \\ a+b+c=-100\rightarrow a=-100-b-c\text{ (1)} \\ \\ 8a+4b+2c+d-d=320-500 \\ 8a+4b+2c=-180\text{ (2)} \\ \\ 27a+9b+3c+d-d=256-500 \\ 27a+9b+3c=-244\text{ (3)} \end{gathered}`

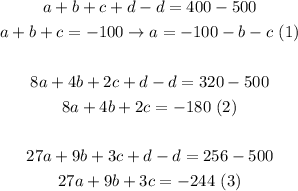
We solve the system of equations as follows:

Replacing (1) in (2) and (3):

`\begin{gathered} 8\cdot(-100-b-c)+4b+2c=-180\rightarrow-4b-6c-800=-180\rightarrow b=-(3c+310)/(2)(4) \\ 27\cdot(-100-b-c)+9b+3c=-244\rightarrow-18b-24c-2700=-244\text{ (5)} \end{gathered}`

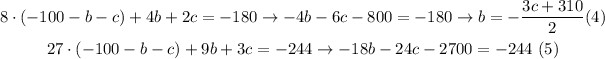
Replacing (4) in (5) and solving for c:

`\begin{gathered} -18\cdot\mleft(-(3c+310)/(2)\mright)-24c-2700=-244 \\ 27c+2790-24c-2700=-244 \\ 3c+90=-244 \\ c=-(334)/(3) \end{gathered}`

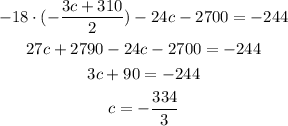
We replace the value of c in (4):

`b=-(3\cdot-(334)/(3)+310)/(2)=-(-334+310)/(2)=-(24)/(2)=-12`

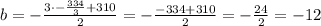
Now we replace the values of b and c in (1):

`\begin{gathered} a=-100-\mleft(12\mright)-\mleft(-(334)/(3)\mright) \\ a=-(2)/(3) \end{gathered}`

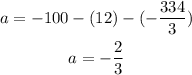
Therefore, the a rule to represent the height of then ball after each bounce is the following:

`h(x)=-(2)/(3)\cdot x^3+12\cdot x^2-(334)/(3)\cdot x+500`

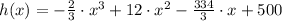
The height after the sixth bounce , would be when x = 6, we replace:

`\begin{gathered} h(6)=-(2)/(3)\cdot6^3+12\cdot6^2-(334)/(3)\cdot6+500 \\ h(6)=-(2)/(3)\cdot216+12\cdot36-334\cdot2+500 \\ h(6)=-144+432-668+500 \\ h(6)=120 \end{gathered}`

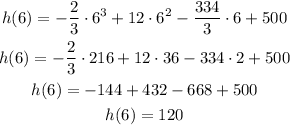
The height after the sixth bounce is 120 meters