we need to find the equation, so when they say is "directly proportional" means that when one variable grows, the other one will grow too. so here we have d (distance) and t^2 (square of the time) and proportional mean:

a is a constant we can calculate
we know when d=87 t=3
so we can replace and find the value of a
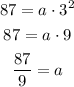
so the equation is
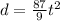
finally, we can replace t=6 and find the distance
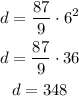
so the answer is: 348 ft