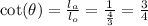If we are working with angles between 0° and 90°, we can use a right triangle to help us visualize the answer.
So, we know that secant is the inverse of cosine, that is:
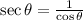
And we know that cosing, in a right triangle, is the adjancet leg divided by the hypotenuse. Let's call l_a the adjacent leg, l_o the opposide leg and h the hypotenuse. So:
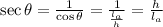
And we know that sec (θ) is 5/3, so if we draw a triangle with l_a = 1, we will have:
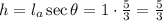
so:
The cot(θ) is the inverse of tan(θ), so:
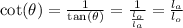
So, we can use the Pythagora's theorem to find l_o and calculate cot(θ):
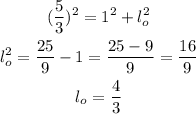
So: