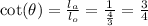Question

help me please. i want to know if im doing it right. if sec (θ) = 5/3 and 0° < θ < 90°, what is cot (θ)?write the answer in simplified rationalized form.

Answer 1

If we are working with angles between 0° and 90°, we can use a right triangle to help us visualize the answer.

So, we know that secant is the inverse of cosine, that is:

`\sec \theta=(1)/(\cos \theta)`

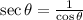
And we know that cosing, in a right triangle, is the adjancet leg divided by the hypotenuse. Let's call l_a the adjacent leg, l_o the opposide leg and h the hypotenuse. So:

`\sec \theta=(1)/(\cos \theta)=(1)/((l_a)/(h))=(h)/(l_a)`

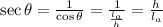
And we know that sec (θ) is 5/3, so if we draw a triangle with l_a = 1, we will have:

`h=l_a\sec \theta=1\cdot(5)/(3)=(5)/(3)`

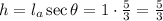
so:

The cot(θ) is the inverse of tan(θ), so:

`\cot (\theta)=(1)/(\tan(\theta))=(1)/((l_o)/(l_a))=(l_a)/(l_o)`

So, we can use the Pythagora's theorem to find l_o and calculate cot(θ):

`\begin{gathered} ((5)/(3))^2=1^2+l^2_o_{} \\ l^2_o=(25)/(9)-1=(25-9)/(9)=(16)/(9) \\ l_o=(4)/(3) \end{gathered}`

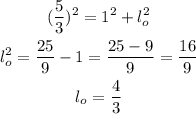
So:

`\cot (\theta)=(l_a)/(l_o)=(1)/((4)/(3))=(3)/(4)`