We can solve this question if we have that the sum of the interior angles of a triangle is 180 degrees.
We have:
Statement-------------------------------------Reasons
The sum of the interior angles of a triangle is equal to 180 degrees. Then, we have:
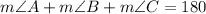
Then, we have that m∠B = 90° (since AB is perpendicular to BC). Then, we have:
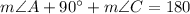
Subtracting 90° from both sides of the equation, we have:
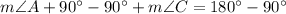
Finally
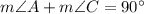
Therefore,
[We have from your homework: "If two angles form a right angle (90°), then they are complementary.]