For this, we are going to use both equations to find the intersection point on both of them. We got:
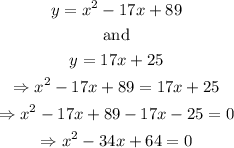
Finally, we find the roots of the polynomial to get the values of x that we need:
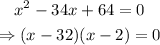
From this, we can see that the roots are x=2 and x=32, therefore, the sales will match on weeks 2 and 32.
Now, to calculate the sales, we use both values of x that we found to get the value of y in both equations:
For x = 2:
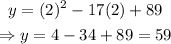
For x=32:
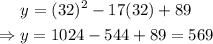
Therefore, the sales on weeks 2 and 32 are 59 and 569 respectively.