Question

The sales of two different products are modeled by the equations shown below. The sales are represented by y and the number of weeks the products have been selling is represented by x. According to the projections what weeks did the products have the same amount of sales? What were the sales of both products during the weeks of equalsales? (Hint: you should have 2 answers chosen for this question. One for the weeks and one for the sales)Product 1 y=x2-17x+89Product 2 y. 17x + 25A.sales: 25B.The sales and weeks never matchC.weeks 2 and 32D.week: 0E.sales: 59 and 569

Answer 1

For this, we are going to use both equations to find the intersection point on both of them. We got:

`\begin{gathered} y=x^2-17x+89 \\ \text{and} \\ y=17x+25 \\ \Rightarrow x^2-17x+89=17x+25 \\ \Rightarrow x^2-17x+89-17x-25=0 \\ \Rightarrow x^2-34x+64=0 \end{gathered}`

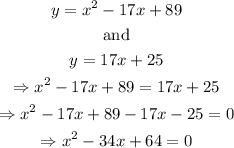
Finally, we find the roots of the polynomial to get the values of x that we need:

`\begin{gathered} x^2-34x+64=0^{} \\ \Rightarrow(x-32)(x-2)=0 \end{gathered}`

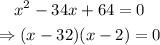
From this, we can see that the roots are x=2 and x=32, therefore, the sales will match on weeks 2 and 32.

Now, to calculate the sales, we use both values of x that we found to get the value of y in both equations:

For x = 2:

`\begin{gathered} y=(2)^2-17(2)+89 \\ \Rightarrow y=4-34+89=59 \end{gathered}`

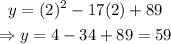
For x=32:

`\begin{gathered} y=(32)^2-17(32)+89 \\ \Rightarrow y=1024-544+89=569 \end{gathered}`

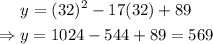
Therefore, the sales on weeks 2 and 32 are 59 and 569 respectively.