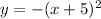Question

The transformations to the parent function of a quadratic equation are given below.Write an equation of the new function in vertex form. Note: ^ denotes "raised to the power of"Transformations: reflected over the x - axis, then translated 5 units leftA y = - (x + 5)^2-1B y = -(x + 5)^2C y = - (x - 5)^2D y = (x + 5)^2

Answer 1

`y=-(x+5)^2`

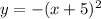
Step-by-step explanation

We have to find the equation of the new function that undergoes the following transformations:

reflected over the x axis and then translated 5 units left.

The parent function of a quadratic equation is:

`y=x^2`

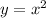
First, we reflect it over the x axis. When you reflect a function over the x axis, it means that for the same values of x, the y values become the negative of the former y values.

This means that the function becomes:

`y=-x^2`

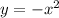
Now, the function is translated 5 units to the left. This means that the y values now have the same value for (x -5), instead of x.

Therefore, the new function is:

`y=-(x+5)^2`

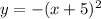
It follows the horizontal translation rule:

`\begin{gathered} y=(x-a)^2 \\ \text{where a = translation factor} \end{gathered}`

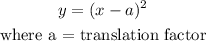
Therefore, the new function is:

`y=-\mleft(x+5\mright)^2`