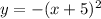ANSWER
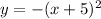
Step-by-step explanation
We have to find the equation of the new function that undergoes the following transformations:
reflected over the x axis and then translated 5 units left.
The parent function of a quadratic equation is:
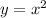
First, we reflect it over the x axis. When you reflect a function over the x axis, it means that for the same values of x, the y values become the negative of the former y values.
This means that the function becomes:
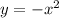
Now, the function is translated 5 units to the left. This means that the y values now have the same value for (x -5), instead of x.
Therefore, the new function is:
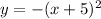
It follows the horizontal translation rule:
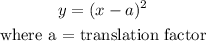
Therefore, the new function is: