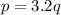Question

If p varies directly as q and p=9.6 when q=3, find the equation that relates p and q.

Answer 1

p varies directly as q,

Mathematically,

`p\propto q`

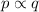
Let us now introduce a constant k,

`\begin{gathered} p\propto kq \\ p=kq \end{gathered}`

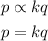
Let us now substitute the values of p and q into the equation and solve for k.

`\begin{gathered} p=9.6 \\ q=3 \end{gathered}`
`\begin{gathered} 9.6=k*3 \\ 9.6=3k \end{gathered}`
`\begin{gathered} \text{divide both sides by 3}, \\ (3k)/(3)=(9.6)/(3) \\ k=3.2 \end{gathered}`

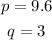
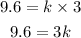
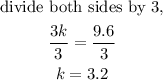
Let us now substitute 3.2 for k back into the equation inorder to get the equation that relates p and q.

Hence, the equation that relates p and q is,

`p=3.2q`