Question

A chef is going to use a mixture of two brands of Italian dressing. The first brand contains 5% vinegar, and the second brand contains 15% vinegar. The chef wants to make 230 milliliters of a dressing that is 9% vinegar. How much of each brand should she use?

Answer 1

Let's say the two brands are Brand A and Brand B.

Brand A: 5% vinegar

Brand B: 15% vinegar

X = amount of Brand A

Y = amount of Brand B

Goal: 230 milliliters of 9% vinegar

See the illustration below.

From the illustration above, we can get the following equations:

First Equation: X + Y = 230 mL

Second Equation: 0.05x + 0.15y = 20.7

(Note: 20.7 here is .09 multiplied to 230)

Now that we have a system of linear equations here, we can now solve for the X and Y (amount of each brand). We can do substitution, elimination, or matrix to solve this. But for this equation, let's use substitution.

Let's equate the first equation into Y:

`\begin{gathered} x+y=230 \\ y=230-x \end{gathered}`

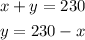
We will substitute y = 230 - x to the second equation.

`\begin{gathered} 0.05x+0.15y=20.7 \\ 0.05x+0.15(230-x)=20.7 \\ 0.05x+34.5-0.15x=20.7 \\ 0.05x-0.15x=20.7-34.5 \\ -0.10x=-13.8 \\ (-0.10x)/(-0.10)=(-13.8)/(-0.10) \\ x=138mL \end{gathered}`

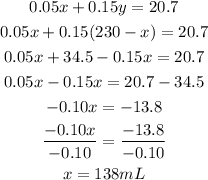
Now that we have the value of x, let's solve the value of y. Substitute the value of x to the first equation.

`\begin{gathered} x+y=230 \\ 138+y=230 \\ y=230-138 \\ y=92mL \end{gathered}`

Therefore, 138 mL of 5% vinegar and 92 mL of 15% vinegar must be combined in order to produce a 230 mL of dressing that is 9% vinegar.