0.274348
Step-by-step explanation
Step 1
in a head-on elastic collision between a small projectile, in this case the neutron, and a much more massive target (atom), the projectile will bounce back with essentially the same speed and the massive target will be given a very small velocity,In elastic head-on collision, the energy of the system and total momentum is conserved
it can be represented by the expression
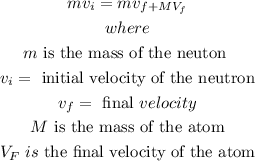
then, let's set the equations
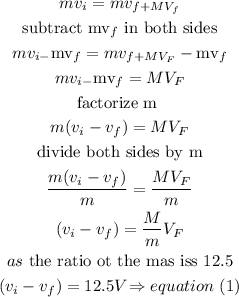
Step 2
the kinetic energy
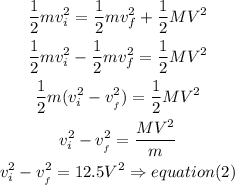
combinde
a)
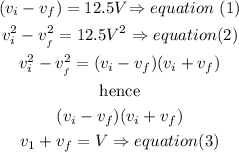
Step 3
solve the equaions
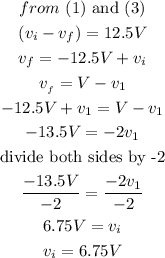
Calculate the fraction of the neutron's kinetic energy transferred to the atomic nucleus.
Let
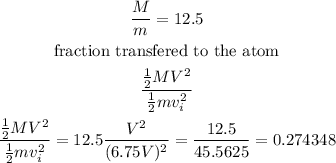
therefore, the answer is 0.274348
I hope this helps you