Question

. Suppose a tortoise is 1000 feet from the ocean. Each day the tortoise travels three-fifths of theremaining distance to the ocean. Use this information to:16. Construct a model that represents the remaining distance that the tortoise must travel to reach the ocean

Answer 1

ANSWER

`r(n)\text{ = 1000}*((2)/(5))^n`

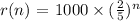
Explanation:

Given information

The tortoise travels three-fifths of the remaining distance to the ocean

The initial distance of tortoise from the ocean = 1000 ft

Step 1: Determine the remaining distance at the end of each day

Let x represents the remaining distance at the end of each day

`\begin{gathered} x\text{ = 1 - }(3)/(5) \\ x\text{ = }\frac{\text{ 5 - 3}}{5} \\ x\text{ = }(2)/(5) \end{gathered}`

Hence, the remaining distance at the end of each day is two-fifths (2/5)

So, the function can be modeled by an exponential with a growth factor of 2/5

Hence, the modeled equation can be written below as

`\begin{gathered} r(n)\text{ = }1000*\text{ (}(2)/(5))^n \\ \text{Where} \\ r(n)\text{ = number of remaining distance (feet) after n days travels} \\ n\text{ = number of days} \end{gathered}`