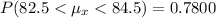We are given the following information
Population mean = μ = 83.3
Population standard deviation = σ = 5.8
Population size = N = 85
Sample size = n = 33
As you can see, the sample size is quite large (n≥30) so the sampling distribution of the sample mean will be approximately normal.
The sample mean will be the same as the population mean.
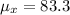
The standard error of the sample will be
![\sigma_x=\frac{\sigma}{\sqrt[]{n}}=\frac{5.8}{\sqrt[]{33}}=1.01](https://img.qammunity.org/2023/formulas/mathematics/college/d0nin2rzf16pfdbczqxvnzkaufkxx2cunp.png)
Now let us multiply this standard error by the correction factor since the sample size (33) is greater than 5% of the population (85)
![CF=\sqrt[]{(N-n)/(N-1)}=\sqrt[]{(85-33)/(85-1)}=0.787](https://img.qammunity.org/2023/formulas/mathematics/college/hmcjzamehmfusordfae0k9509wqko1oeee.png)
So, the standard error after the correction is
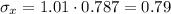
b. Sample mean less than 85
The probability that the sample mean will be less than 85 is given by
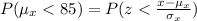
The Excel function is given by
=NORM.DIST(x, mean, standard error, TRUE)
So, substituting the values, it becomes
=NORM.DIST(85, 83.3, 0.79, TRUE)
Excel returns the following probability
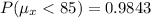
c. Sample mean more than 84
The probability that the sample mean will be more than 84 is given by
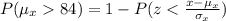
Using Excel,
=NORM.DIST(84, 83.3, 0.79, TRUE)
Now subtract the result from 1
1 - 0.8122 = 0.1878
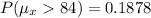
d. sample mean between 82.5 and 84.5
The probability that the sample mean will be between 82.5 and 84.5 is given by
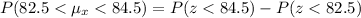
Using Excel,
=NORM.DIST(84.5, 83.3, 0.79, TRUE)
0.9356
=NORM.DIST(82.5, 83.3, 0.79, TRUE)
0.1556
So, the probability is
0.9356 - 0.1556 = 0.78