The perimater of the garden is P=60 feet
The length is twice its width.
Let "x" represent the measure of the width of the garden, then:
w=x
l= 2x
The formula to calculate the perimeter is:
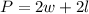
Replace it with the determined equalities, and you get that the perimeter of the garden is equal to:
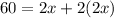
From this expression you can calculate the value of x

w=x=10 feet
l=2x=2*10=20 feet
The width of the garden is w=10 feet and the length of the garden is l=20 feet