If the decay ratio is 2% each year, there is left 98%, which is 0.98.
Then, if the initial mass is 50 kilograms, then we can express the following
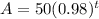
Then, we solve for t, when A = 25, which is half of the initial amount.
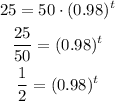
Now, we use logarithms to find the value of t

Hence, the time that it takes for only half of the initial amount is 34.3 years.