From the given graph we can observe that there are three parallel lines.
Also, angle (8x-7) and (3x-11) are same-side interior angles which means they are supplementary, the sum 180°.-
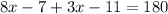
We solve for x.
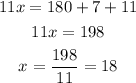
Additionally, from the given graph, we deduct that angles (2y+23) and (4y+8) are alternate interior angles that are congruent.
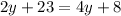
We solve for y.
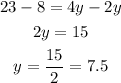
Then, angles 2y+23 and 3z2 - 5 are supplementary angles, they sum 180°.
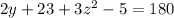
Let's replace y and solve for z.
![\begin{gathered} 2(7.5)+23+3z^2-5=180 \\ 15+3z^2+18=180 \\ 3z^2=180-15-18 \\ z^2=(147)/(3)=49 \\ z=\sqrt[]{49}=7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sxdck3i6lri2qx2q5vwbzf11u1d7nllokd.png)
Therefore, the variables are equal to x = 18, y = 7.5, and z = 7.