Question

Find the values of x, y, and z in the figure, given z> 0

Answer 1

From the given graph we can observe that there are three parallel lines.

Also, angle (8x-7) and (3x-11) are same-side interior angles which means they are supplementary, the sum 180°.-

`8x-7+3x-11=180`

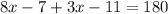
We solve for x.

`\begin{gathered} 11x=180+7+11 \\ 11x=198 \\ x=(198)/(11)=18 \end{gathered}`

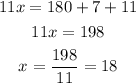
Additionally, from the given graph, we deduct that angles (2y+23) and (4y+8) are alternate interior angles that are congruent.

`2y+23=4y+8`

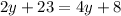
We solve for y.

`\begin{gathered} 23-8=4y-2y \\ 2y=15 \\ y=(15)/(2)=7.5 \end{gathered}`

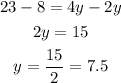
Then, angles 2y+23 and 3z2 - 5 are supplementary angles, they sum 180°.

`2y+23+3z^2-5=180`

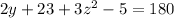
Let's replace y and solve for z.

`\begin{gathered} 2(7.5)+23+3z^2-5=180 \\ 15+3z^2+18=180 \\ 3z^2=180-15-18 \\ z^2=(147)/(3)=49 \\ z=\sqrt[]{49}=7 \end{gathered}`

Therefore, the variables are equal to x = 18, y = 7.5, and z = 7.