Question

Solve the absolute value equation l2x+3l+4=1

Answer 1

The given equation is

`|2x+3|+4=1`

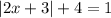
First, we need to isolate the absolute value, we'll subtract 4 one each side

`\begin{gathered} |2x+3|+4-4=1-4 \\ |2x+3|=-3 \end{gathered}`

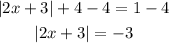
Now, we rewrite the equation in two equations

`\begin{gathered} 2x+3=-3 \\ 2x+3=-(-3)\rightarrow2x+3=3 \end{gathered}`

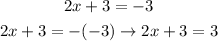
Let's solve each equation

`\begin{gathered} 2x+3=-3 \\ 2x=-3-3 \\ 2x=-6 \\ x=-(6)/(2)=-3 \end{gathered}`

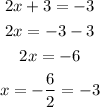
So, the first solution is -3.

`\begin{gathered} 2x+3=3 \\ 2x=3-3=0 \\ x=(0)/(2)=0 \end{gathered}`

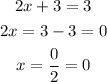
The second solution is zero.

Therefore, the solutions are -3, and 0.