The given equation is
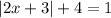
First, we need to isolate the absolute value, we'll subtract 4 one each side
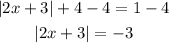
Now, we rewrite the equation in two equations
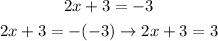
Let's solve each equation
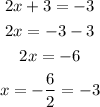
So, the first solution is -3.

The second solution is zero.
Therefore, the solutions are -3, and 0.