Question

Solve the rational equation for x and state all x values that are excluded from the solution set. If there is more than one excluded value then separate them with a comma and do not include any spaces. \frac{3}{x-2}=\frac{1}{x-1}+\frac{7}{(x-1)(x-2)} Solving for x gives us x=AnswerThe value for x cannot equal Answer

Answer 1

The equation to solve is,

`(3)/(x-2)=(1)/(x-1)+(7)/((x-1)(x-2))`

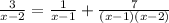
Let's use algebra to simplify the equation and solve for 'x'. The steps are shown below:

`\begin{gathered} (3)/(x-2)=(1)/(x-1)+(7)/((x-1)(x-2)) \\ (3)/(x-2)=(1(x-2)+7)/((x-1)(x-2)) \\ (3)/(x-2)=(x-2+7)/((x-1)(x-2)) \\ (3)/(x-2)=(x+5)/((x-1)(x-2)) \\ \text{Cross Multiplication >>>>} \\ 3(x-1)(x-2)=(x-2)(x+5) \\ 3\lbrack x^2-3x+2\rbrack=x^2+3x-10 \\ 3x^2-9x+6=x^2+3x-10 \\ 3x^2-9x+6-x^2-3x+10=0 \\ 2x^2-12x+16=0 \\ x^2-6x+8=0 \\ (x-2)(x-4)=0 \\ x=2,4 \end{gathered}`

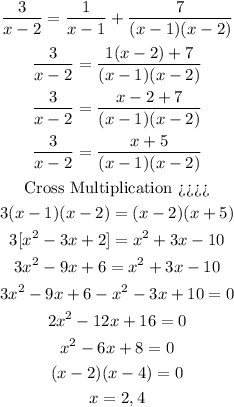
The solution is x = 2 and x = 4.

Looking back at the original question, we can see that we cannot put x = 2 into the equation. It will make the denominator equal to 0. So, we disregard this value of x.

Thus, the only solution is 'x = 4'.

AnswerSolving for x gives us x = 4The value of x cannot equal 2