The equation to solve is,
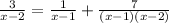
Let's use algebra to simplify the equation and solve for 'x'. The steps are shown below:
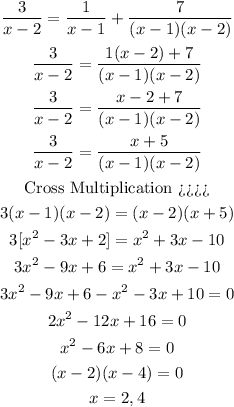
The solution is x = 2 and x = 4.
Looking back at the original question, we can see that we cannot put x = 2 into the equation. It will make the denominator equal to 0. So, we disregard this value of x.
Thus, the only solution is 'x = 4'.
AnswerSolving for
x gives us
x = 4The value of
x cannot equal 2