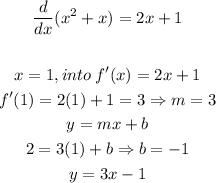Question

Answer the derivative without power laws. We must use this equation to find the derivative: ( f(x + h) - f(x) ) / hAlso help find the tangent lines

Answer 1

`\begin{gathered} i)f^(\prime)(x)=(1)/(2√(x+4)),\:y=(1)/(4)x+2 \\ ii)f^(\prime)(x)=2x+1,\:y=3x-1 \end{gathered}`

1) When we resort to the definition of a derivative we use the following model to get the 1st derivative:

`\begin{gathered} \lim _(h\to 0)\left[(f\left(x+h\right)−f\left(x\right))/(h)\right] \\ \lim _(h\to \:0)\left((√(x+h+4)-√(x+4))/(h)\right) \\ =\lim_(h\to\:0)\left(((h)/(√(x+h+4)+√(x+4)))/(h)\right)\:\:Multiply\:by\:the\:conjugate: \\ (\left(√(x+h+4)-√(x+4)\right)\left(√(x+h+4)+√(x+4)\right))/(√(x+h+4)+√(x+4)) \\ (h)/(√(x+h+4)+√(x+4)) \\ \mathrm{Plug\:in\:the\:value}\:h=0 \\ (1)/(√(0+x+4)+√(x+4)) \\ (1)/(2√(x+4)) \\ \end{gathered}`

Note that we had to apply some limit properties as well as multiplication by the conjugate. In the end, we plug into that h=0 to get the derivative.

1.2) Now, let's find the tangent line at P(0,2)

Let's start out with the slope since we already know the 1st derivative, then we can write it out right away, that will save some time.

`\begin{gathered} (d)/(dx)\left(√(x+4)\right)=(1)/(2√(x+4)) \\ \end{gathered}`

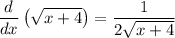
Now, let's plug into the original equation x=0 , since the point is (0,2):

`\begin{gathered} f^(\prime)(x)=(1)/(2√(x+4)) \\ f^(\prime)(0)=(1)/(2√(0+4))=(1)/(2√(4))=(1)/(4) \\ m=(1)/(4) \end{gathered}`

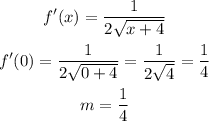
We can tell the slope is 1/4. So now, resorting to the slope-intercept form we can plug the y-coordinate to find the y-intercept

`\begin{gathered} m=(1)/(4),(0,2) \\ y=mx+b \\ 2=(1)/(4)(0)+b \\ b=2 \\ ---- \\ Tangent\:line:\:y=(1)/(4)x+2 \end{gathered}`

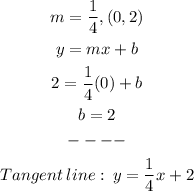
b) Let's find the derivative using the definition for the function: f(x)=x²+x

`\begin{gathered} \lim _(h\to \:0)\left((\left(x+h\right)^2+x+h-\left(x^2+x\right))/(h)\right) \\ (\left(x+h\right)^2+x+h-\left(x^2+x\right))/(h) \\ (x^2+2xh+h^2+x+h-\left(x^2+x\right))/(h) \\ (2hx+h^2+h)/(h) \\ (h\left(2x+h+1\right))/(h) \\ 2x+h+1 \\ 2x+0+1 \\ 2x+1 \end{gathered}`

And now the tangent line at point (1,2)

`\begin{gathered} (d)/(dx)(x^2+x)=2x+1 \\ \\ x=1,into\:f^(\prime)(x)=2x+1 \\ f^(\prime)(1)=2(1)+1=3\Rightarrow m=3 \\ y=mx+b \\ 2=3(1)+b\Rightarrow b=-1 \\ y=3x-1 \end{gathered}`