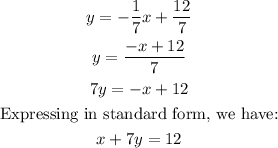Question

indicate in standard form the equation of the line passing through the given pointsE(-2,2),P(5,1)enter your answer in the blank question box

Answer 1

x+7y=12

Step-by-step explanation:

The standard form of the equation of a line is: ax+by=c

To determine the equation of the line passing through E(-2,2) and P(5,1).

First, we determine the slope.

`\begin{gathered} \text{Slope}=\frac{Change\text{ in y}}{Change\text{ in x}} \\ =(1-2)/(5-(-2)) \\ =(-1)/(7) \\ m=-(1)/(7) \end{gathered}`

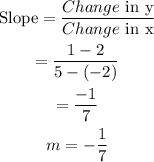
Next, we determine the y-intercept.

Using the point (5,1)

When x=5, y=1

`\begin{gathered} y=mx+b \\ 1=-(1)/(7)(5)+b \\ b=1+(5)/(7) \\ b=(12)/(7) \end{gathered}`

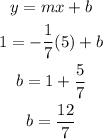
Therefore, the equation of the line is:

`\begin{gathered} y=-(1)/(7)x+(12)/(7) \\ y=(-x+12)/(7) \\ 7y=-x+12 \\ \text{Expressing in standard form, we have:} \\ x+7y=12 \end{gathered}`