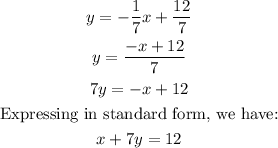Answer:
x+7y=12
Step-by-step explanation:
The standard form of the equation of a line is: ax+by=c
To determine the equation of the line passing through E(-2,2) and P(5,1).
First, we determine the slope.
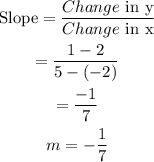
Next, we determine the y-intercept.
Using the point (5,1)
When x=5, y=1
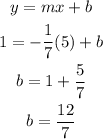
Therefore, the equation of the line is: