Question

Given a function f (x) = 3x2 + 4, what is the average rate of change of f on the interval [2, 2 + h]?3h + 123h2 + 12h3h2 + 12h + 1616

Answer 1

We are given the following function:

`f(x)=3x^2+4`

We are asked to determine the average rate of change on the interval [2, 2 + h]. To do that we will use the following formula:

`r=(f(b)-f(a))/(b-a)`

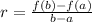
in the interval:

`\lbrack a,b\rbrack`

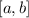
Therefore, we need to evaluate the function at the points x = 2 and x = 2 + h. Evaluating in x = 2 we get:

`f(2)=3(2)^2+4=16`

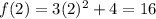
Now we evaluate at x = 2 + h:

`f(2+h)=3(2+h)^2+4`

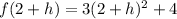
Now we solve the square:

`f(2+h)=3(4+4h+h^2)+4`

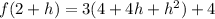
Now we apply the distributive property:

`f(2+h)=12+12h+3h^2+4=12h+3h^2+16`

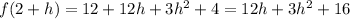
Now we use the average rate of change formula:

`r=(f(2+h)-f(2))/((2+h)-(2))`

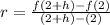
Substituting the values:

`r=(12h+3h^2+16-16)/(h)`

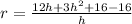
Simplifying:

`r=(12h+3h^2)/(h)`

Now we take common factor on the numerator:

`r=(h(12+3h))/(h)`

We can cancel out the "h":

`r=12+3h`

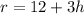
Therefore, the average rate of change is 12 + 3h.