Let D, R, and I, denote the set of politicians being Democrats, Republicans, and Independents.
According to the given problem,
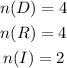
Consider that the probability of an event is given by,

As per the given problem, the favourable event is that the two selected politicians at succession are not Independents.
The number of ways of selecting 2 politicians such that both of them are Independents,
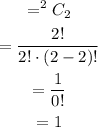
So there is only 1 favourable outcome.
The total number of ways of selecting 2 politicians from the group is,
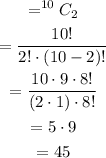
Then the corresponding probability is given by,