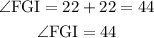Question

In the diagram, GH bisects

Answer 1

a)

Angles FGH and HGI are equal [since GH bisects Angle FGI].

We can equate their algebraic expressions and solve for x first. Shown below:

`\begin{gathered} \angle\text{FGH}=\angle\text{HGI} \\ 2x-8=3x-23 \\ -8+23=3x-2x \\ 15=x \end{gathered}`

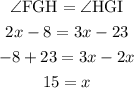
b)

We want to find Angle FGH, 2x - 8, found x = 15.

`\begin{gathered} \angle\text{FGH}=2x-8 \\ =2(15)-8 \\ =30-8 \\ =22\degree \end{gathered}`

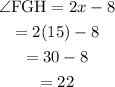
c)

We want to find HGI. Similar process as b). Shown below:

`\begin{gathered} \angle\text{HGI}=3x-23 \\ =3(15)-23 \\ =45-23 \\ =22\degree \end{gathered}`

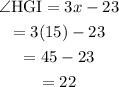
d)

Angle FGI is the sum of Angle FGH and Angle HGI, which are both found to be 22 each.

Thus,

`\begin{gathered} \angle\text{FGI}=22+22=44 \\ \angle\text{FGI}=44\degree \end{gathered}`