The given expression :
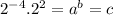
We have to find the value of c,
The exponents can aslo express as :
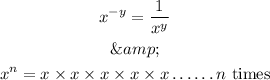
and if the base of the exponents are equal then the exponents value will simplify
i.e if they are multiply then the exponents will sum up
and if they divide then the exponents will subtract (Denominator exponent value is subtracted from Numerator exponent value)
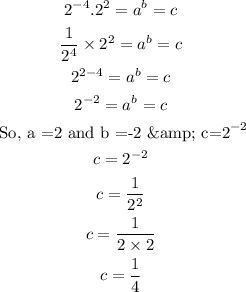
Answer : D) 1/4