In the right triangles whose legs are a, b and its hypotenuse is c

In triangle JLK
∵ LK and JL are the legs of the triangle
∵ KJ is the hypotenuse
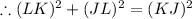
∵ KL = 14 m and KJ = 18 m
Substitute them in the rule above to find JL
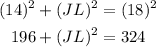
Subtract 196 from both sides
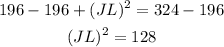
Take a square root for both sides
![\begin{gathered} \sqrt[]{(JL)^2}=\sqrt[]{128} \\ JL=11.3137085 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qd7gd4l5z9vq3mtawu3l1il5csamshx8em.png)
Round it to the nearest hundredth
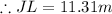
The answer is 11.31 m