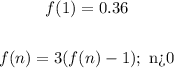Given the table:
n 0 1 2 3
f(n) 0.12 0.36 1.08 3.24
Let's write the explicit and recursive rule for the sequence.
Let's determine if the sequence is a geometric sequence.
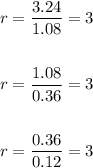
The sequence has a common ratio of 3.
Therefore, it is a geometric sequence.
For the explicit formula of a geometric sequence, apply the formula:
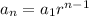
Where:
a1 is the first term = 0.36
r is the common ratio = 3
Hence, we have the explicit rule:
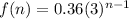
• Recursive rule:
Form the recursive rule of a sequence, we have:
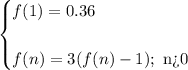
ANSWER:
• Explicit formula:
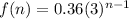
• Recursive formula: