Let x represent the number of trees of corn muffins
Let y represent the number of trees of bran muffins
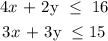
Then reducing it to the simplest form
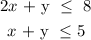
Then the number of corn muffins with bran muffins to make a profit
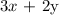
where
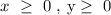
The graph showing all points of x and y values to be tested to obtain the maximum profit is given below
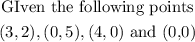
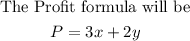
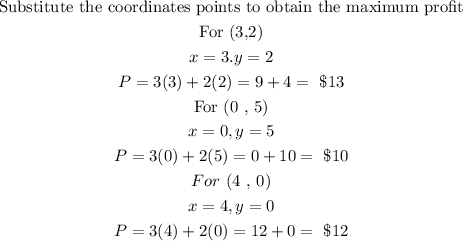
From the above test, the points that yield the maximum profit is at ( 3, 2), therefore we can conclude that the baker would need 3 trays of corn muffins and 2 trays of bran muffins to maximize his profit
The answer is 3 trays of corn muffins and 2 trays of bran muffins