The equation of a circle is given by the expression
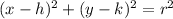
Where (h,k) is the center and r is the radius.
We have 2 points that happen to define the diameter of the circle. In order to obtain the radius we need the distance between those 2 points:
![D=d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/v45wa9i6zue0vm3jfsqhdzivjhcuroeie1.png)
This is the formula to obtain the distance between two points on the plane. We proceed by filling that formula with the information given by the problem
![D=\sqrt[]{(6-4)^2+(-5-3)^2}=\sqrt[]{2^2+(-8)^2}=\sqrt[]{68}=\sqrt[]{4\cdot17}=2\sqrt[]{17}](https://img.qammunity.org/2023/formulas/mathematics/college/7v71hjpiebmiqgrf4ur3ohii4po2luqot3.png)
That's the diameter, the radius is D/2
![r=(D)/(2)=\frac{2\sqrt[]{17}}{2}=\sqrt[]{17}](https://img.qammunity.org/2023/formulas/mathematics/college/wp3u9t26ca4ly3yd7vwtib616389b8rymm.png)
Finally, we need to find the center of the circumference. For this, we need the middle point of the segment that joins the two given points since we know those define a diameter.
The middle point is given by the formula
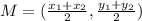
Using the information of our particular problem, we get
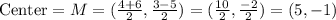
So, the center of the circle is (5,-1)
Finally, we have everything we need to use the first formula in the explanation:
(h,k)=(5,-1) and r=(17)^(1/2)
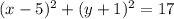
This last result is the answer to our problem