Question

Write an equation of the circle whose diameter has endpoints (4,3) and (6,-5) please

Answer 1

The equation of a circle is given by the expression

`(x-h)^2+(y-k)^2=r^2`

Where (h,k) is the center and r is the radius.

We have 2 points that happen to define the diameter of the circle. In order to obtain the radius we need the distance between those 2 points:

`D=d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

This is the formula to obtain the distance between two points on the plane. We proceed by filling that formula with the information given by the problem

`D=\sqrt[]{(6-4)^2+(-5-3)^2}=\sqrt[]{2^2+(-8)^2}=\sqrt[]{68}=\sqrt[]{4\cdot17}=2\sqrt[]{17}`

That's the diameter, the radius is D/2

`r=(D)/(2)=\frac{2\sqrt[]{17}}{2}=\sqrt[]{17}`

Finally, we need to find the center of the circumference. For this, we need the middle point of the segment that joins the two given points since we know those define a diameter.

The middle point is given by the formula

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

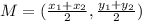
Using the information of our particular problem, we get

`\text{Center}=M=((4+6)/(2),(3-5)/(2))=((10)/(2),(-2)/(2))=(5,-1)`

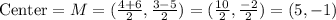
So, the center of the circle is (5,-1)

Finally, we have everything we need to use the first formula in the explanation:

(h,k)=(5,-1) and r=(17)^(1/2)

`(x-5)^2+(y+1)^2=17`

This last result is the answer to our problem