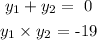y1 + y2 = 0
y1*y2 = -19
Step-by-step explanation:
The equation: y^2 - 19 = 0
Using Vieta's formula for equation in the form:
ax^2 + bx + c = 0
sum of roots = -b/a
Product of roots = c/a
Comparing the equation above with the equation in the question:
y^2 + 0x -19 = 0
coefficent of y^2 = a = 1
coefficient of x = b = 0
The constant = c = -19
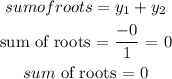

Hence: