SOLUTION
Write out the data given
To construct a frequency table, we write out the data and obtain thier frquency.
The data ranges from 150 to 156, we write 150 to 156 vertically,
The probability of an event is given by the required outcome of the total outcome,
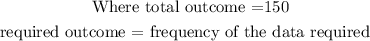
Hence, the probabilty that the height of the student is not more that 153 will be

Where
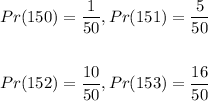
Then, take the sum of the probability, we have
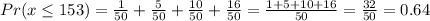
hence
The probability that if a student is chosen at random that he/she is not more than 153cm in height is 32/50 or 0.64
Similartly, The probability that the height is greater than 153 will be
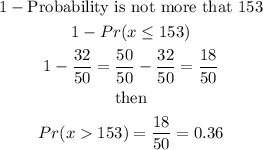
Hence
The probability that the height is greater than 153 in height is 18/50 or 0.36