Question

A 6kg block is placed near the top of a frictionless ramp, which makes an angle of 30 degree to the horizontal. A distance of d=1.4m away from the block is an unstretched spring with k=2000N/m. The block slides down the ramp and compresses the spring. 1) Find the maximum compression of the spring (Xmax)?

Answer 1

Xmax = 0.21 m

Step-by-step explanation:

If X is the maximum compression of the spring and h is the initial height of the spring with respect to its final position, we get:

It means that the block starts with gravitational potential energy and ends with elastic potential energy. So, by the conservation of Energy:

`\begin{gathered} E_i=E_f \\ \text{mgh}=(1)/(2)kx^2 \end{gathered}`

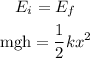
Where m is the mass, g is the gravity and k is the spring constant.

Additionally, h = (d + x)sin30, so we can rewrite the equation as:

`\begin{gathered} mg(d+x)\sin 30=(1)/(2)kx^2 \\ mg(d+x)((1)/(2))=(1)/(2)kx^2 \\ mg(d+x)=kx^2 \\ kx^2-mg(d+x)=0 \end{gathered}`

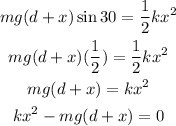
So, replacing the values, we get:

`\begin{gathered} kx^2-mgx-mgd=0 \\ 2000x^2-6(9.8)x-6(9.8)(1.4)=0 \\ 2000x^2-58.8x-82.32=0 \end{gathered}`

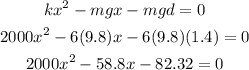
Now, using the quadratic equation, we can solve for x:

`\begin{gathered} x=\frac{58.8\pm\sqrt[]{58.8^2-4(2000)(-82.2)}}{2(2000)} \\ x=0.22 \\ or \\ x=-0.19 \end{gathered}`

Therefore, the maximum compression of the spring will be Xmax = 0.22 m.