A Tv set with an aspect ratio of 16:9 (that is , ratio 16 to 9) has its dimensions such that if the width is divided into 16 parts, then the length would be divided into 9 parts of the same unit.
The screen size is usually the length across the diagonal That is the hypotenuse. Using a 16:9 ratio we shall determine the actual length and width, since the hypotenuse is already known.
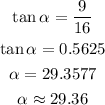
Having calculated one of the side angles as 29.36 degrees, the other angle would measure as follows;

This means if the Tv set were to be split into two along the diagonal, the angles would be 90, 60.64 and 29.36. With these angles and the hypotenuse already known (48 inches), we can calculate the sides as

The other side is calculated as;

Rounded the nearest tenth, the dimensions are now,
Length = 23.5
Width = 41.8
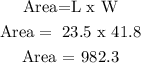
The area of the TV rounded to the nearest tenth is now 982.3