Question

Determine the area of the screen of a newer 48-inch television whose screen has an aspect ratio of 16:9The area is ___ in²(Dont include units and round to nearest tenth)

Answer 1

A Tv set with an aspect ratio of 16:9 (that is , ratio 16 to 9) has its dimensions such that if the width is divided into 16 parts, then the length would be divided into 9 parts of the same unit.

The screen size is usually the length across the diagonal That is the hypotenuse. Using a 16:9 ratio we shall determine the actual length and width, since the hypotenuse is already known.

`\begin{gathered} \tan \alpha=(9)/(16) \\ \tan \alpha=0.5625 \\ \alpha=29.3577 \\ \alpha\approx29.36 \end{gathered}`

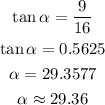
Having calculated one of the side angles as 29.36 degrees, the other angle would measure as follows;

`\begin{gathered} 29.36+\beta+90=180 \\ \beta=180-90-29.36 \\ \beta=60.64 \end{gathered}`

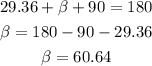
This means if the Tv set were to be split into two along the diagonal, the angles would be 90, 60.64 and 29.36. With these angles and the hypotenuse already known (48 inches), we can calculate the sides as

`\begin{gathered} \sin 60.64=(opp)/(hyp) \\ \sin 60.64=(opp)/(48) \\ \sin 60.64*48=opp \\ 0.8716*48=\text{opp} \\ 41.8368=\text{opp} \end{gathered}`

The other side is calculated as;

`\begin{gathered} \sin 29.36=(opp)/(hyp) \\ \sin 29.36=(opp)/(48) \\ 0.4903*48=\text{opp} \\ 23.5344=\text{opp} \end{gathered}`

Rounded the nearest tenth, the dimensions are now,

Length = 23.5

Width = 41.8

`\begin{gathered} \text{Area=L x W} \\ \text{Area}=\text{ 23.5 x 41.8} \\ \text{Area = 982.3} \end{gathered}`

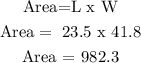
The area of the TV rounded to the nearest tenth is now 982.3