Question

Quadrilateral A B C D has vertices a (1,0) , b (5,0) c(7,2), and d (3,2). Use slope to prove that A B C Dis a parallelogram. Show all of your work.

Answer 1

Given the quadrilateral ABCD with vertices A (1,0) , B (5,0), C(7,2), and D (3,2).

Consider the drawing below

To prove that the quadrilateral is a parallelogram it is sufficient to prove that parallel.

Using slope property

The slope of parallel sides are equal

Finding the slope of side AB

Using the given points

`\text{slope AB}=(0-0)/(5-1)=0`

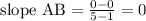
Finding the slope of side CD

`\text{Slope CD}=(2-2)/(7-3)=0`

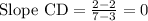
Since the slope of side AB = Slope of side CD

Hence, sides AB and CD are parallel.

Using the same steps

`\begin{gathered} \text{Slope AD}=(2-0)/(3-1)=(2)/(2)=1 \\ \text{Slope BC}=(2-0)/(7-5)=(2)/(2)=1 \end{gathered}`

Also

Since the slope of side BC = Slope of side AD

Hence, sides BC and AD are parallel.

Therefore, the quadrilateral is a parallelogram.