Question

find the dimensions of a rectangular lot whose perimeter is 40 meters and whose area is 96 square meters.

Answer 1

We can use a system of equations to solve this problem.

Taking x and y as the dimensions of the rectangle, we know that the sum of twice each dimension is the perimeter of the rectangle:

`2x+2y=40`

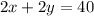
The area of the rectangle is the product of its dimensions:

`xy=96`

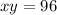
Solve the first equation for y:

`\begin{gathered} 2x+2y=40 \\ 2y=40-2x \\ y=(40-2x)/(2) \\ y=20-x \end{gathered}`

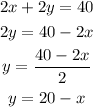
Replace y for this expression in the second equation:

`\begin{gathered} x(20-x)=96 \\ 20x-x^2=96 \end{gathered}`

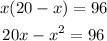
We obtain a quadratic equation that we need to solve:

`\begin{gathered} 0=x^2-20x+96 \\ 0=(x-8)(x-12) \\ x-8=0 \\ x=8 \\ x-12=0 \\ x=12 \end{gathered}`

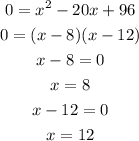
It means that x can be 8 or 12.

Use each value of x to find y:

`\begin{gathered} y=20-x \\ y=20-8 \\ y=12 \\ y=20-12 \\ y=8 \end{gathered}`

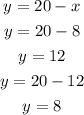
It means that y can be 12 or 8.

According to the results, the dimensions of the rectangular lot are 8 and 12.