We can use a system of equations to solve this problem.
Taking x and y as the dimensions of the rectangle, we know that the sum of twice each dimension is the perimeter of the rectangle:
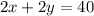
The area of the rectangle is the product of its dimensions:
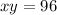
Solve the first equation for y:
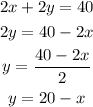
Replace y for this expression in the second equation:
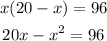
We obtain a quadratic equation that we need to solve:
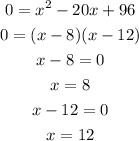
It means that x can be 8 or 12.
Use each value of x to find y:
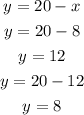
It means that y can be 12 or 8.
According to the results, the dimensions of the rectangular lot are 8 and 12.