Question

A quadratic is defined by f(x) = x2 + 5x - 1. A linear function is defined by g(x) = x - m. Whatvalue of m would make the functions intersect at one point?

Answer 1

m = 5

Step-by-step explanation

If two functions intersect, then both functions have the same value. In this case, we have a quadratic function and a linear function and we have to find the value of m to make these two functions intersect at only one point. If this happens, then the linear function is tangent to the quadratic function.

As we can see, the slope of the linear function is 1, so the derivative of the quadratic function is 1 at that point. With this information, we can find the value of x where these two functions intersect at one point.

The derivative of the quadratic function is,

`f^(\prime)(x)=2x+5`

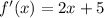
If f'(x) is 1, solve for x,

`2x+5=1\text{ }\Rightarrow\text{ }x=(1-5)/(2)=(-4)/(2)=-2`

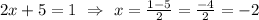
Thus, f(-2) = g(-2),

`\begin{gathered} f(-2)=g(-2) \\ (-2)^2+5(-2)-1=(-2)-m \end{gathered}`

Solve the left side of the equation.

`\begin{gathered} 4-10-1=-2-m \\ -7=-2-m \end{gathered}`

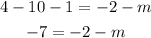
Solving for m,

`m=-2+7=5`

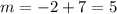
Hence, for m = 5 the functions intersect at one point.