Answer
a) 210
b) 1260
c) 252
Step-by-step explanation
The problem of choosing a number of options from a bigger number of options with the order of the choices not important is solved using Combination.
The number of ways for picking r options from n choices with order not important is given as
ⁿCᵣ
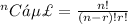
a) n = 10 players
r = 4 players
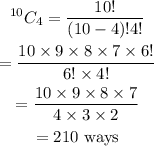
b) n₁ = 10, n₂ = 8 (after the first two have been selected, there are 8 options left)
r₁ = 2; r₂ = 2
c) n₁ = 10, n₂ = 5 (after the first two have been selected, there are 5 options left)
r₁ = 5, r₂ = 5
So, the number of ways will be equal to
= ¹⁰C₅ × ⁵C₅
= [10!/(10 - 5)!5!] × [5!/(5 - 5)!5!]
= [10!/5!5!] × [5!/0!5!]
Noting that 0! = 1
[10!/5!5!] × [5!/0!5!]
= 252 × 1
= 252 ways
Hope this Helps!!!