Question

Ifthereare10playersonabasketballteam,findthenumberofchoicesacoachhastochoosethefollowing:a) 4playerstocarrytheteamequipment.b) 2guardsand2forwards.c) 5startersand5subs.

Answer 1

a) 210

b) 1260

c) 252

Step-by-step explanation

The problem of choosing a number of options from a bigger number of options with the order of the choices not important is solved using Combination.

The number of ways for picking r options from n choices with order not important is given as

ⁿCᵣ

`^(n)Cᵣ=(n!)/((n-r)!r!)`

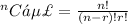
a) n = 10 players

r = 4 players

`\begin{gathered} ^(10)C_4=(10!)/((10-4)!4!) \\ =(10*9*8*7*6!)/(6!*4!) \\ =(10*9*8*7)/(4*3*2) \\ =210\text{ ways} \end{gathered}`

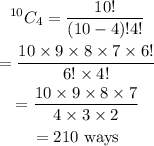
b) n₁ = 10, n₂ = 8 (after the first two have been selected, there are 8 options left)

r₁ = 2; r₂ = 2

`\begin{gathered} \\ =^(10)C_2*^8C_2 \\ =(10!)/((10-2)!2!)*(8!)/((8-2)!2!) \\ =(10!)/(8!2!)*(8!)/(6!2!) \\ =(10*9*8!)/(8!*2)*(8*7*6!)/(6!*2) \\ =(10*9)/(2)*(8*7)/(2) \\ =45*28 \\ =1260 \end{gathered}`

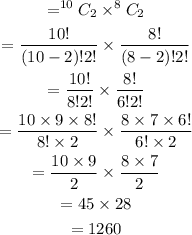
c) n₁ = 10, n₂ = 5 (after the first two have been selected, there are 5 options left)

r₁ = 5, r₂ = 5

So, the number of ways will be equal to

= ¹⁰C₅ × ⁵C₅

= [10!/(10 - 5)!5!] × [5!/(5 - 5)!5!]

= [10!/5!5!] × [5!/0!5!]

Noting that 0! = 1

[10!/5!5!] × [5!/0!5!]

= 252 × 1

= 252 ways

Hope this Helps!!!