Question

2. Given the measures of the sides of a triangle below, which set could form a right triangle?A. 6, 7, 8B. 9, 12, 15C. 12, 15, 20D. 20, 25, 30

Answer 1

A Right triangle is a triangle that has an angle whose measure is 90 degrees.

The Pythagorean Theorem states that:

`a^2=b^2+c^2`

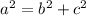
Where "a" is the hypotenuse (the longest side of the Right triangle) and "b" and "c" are the legs of the triangle.

Knowing the above, you can check each set:

Set A

`6,7,8`

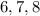
Notice that the longest side is 8. Then:

`\begin{gathered} 8^2=6^2+7^2 \\ 64\\e85 \end{gathered}`

This set couldn't form a Right triangle.

Set B

`9,12,15`

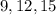
The longest side is 15. Then:

`\begin{gathered} 15^2=9^2+12^2 \\ 225=225 \end{gathered}`

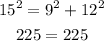
This set could form a Right triangle.

Set C

`12,15,20`

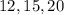
Knowing that the longest side is 20, you get:

`\begin{gathered} 20^2=12^2+15^2 \\ 400\\e369 \end{gathered}`

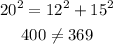
This set couldn't form a Right triangle.

Set D

`20,25,30`

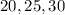
The longest side is 30. Then:

`\begin{gathered} 30^2=20^2+25^2 \\ 900\\e1025 \end{gathered}`

This set couldn't form a Right triangle.

The answer is: Option B.