For this problem we are informed the prices of the tickets for children and adults to a museum. We are also informed that on a certain day twice as many adults bought tickets in comparison to children, and that the total in sales was equal to $778.6. From this information, we need to determine how many child tickets were sold.
The first step we need to take is write the relation between the number of child tickets sold, and the number of adults tickets sold. This is done below:
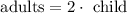
Now we need to write the expression that relates the total income for that day with the number of tickets sold. This is done by multiplying the total of tickets for a certain type with each cost, then adding both.
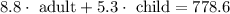
We can use the first expression, and replace it on the second one. This will leave us with only one variable.
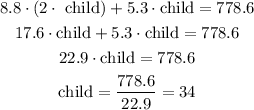
A total of 34 child tickets were sold that day.