Question

The Royal Fruit Company produces two types of fruit drinks. The first type is 40% pure fruit juice, and the second type is 90% pure fruit juice. The company isattempting to produce a fruit drink that contains 75% pure fruit juice. How many pints of each of the two existing types of drink must be used to make 140pints of a mixture that is 75% pure fruit juice?Note that the ALEKS graphing calculator can be used to make computations easier

Answer 1

Let x pints be first type pure fruit juice and y pints be second type pure fruit juice.

The total pints of a mixture is 140, so equation is,

`x+y=140`

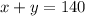
The 40% of first juice is 0.4x and 90% of second type fruit juice is 0.9y. The total mixture has 75% pure fruit juice means,

`\begin{gathered} 0.4x+0.9y=(75)/(100)\cdot140 \\ 0.4x+0.9y=105 \end{gathered}`

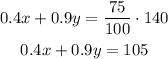
Plot the equation x + y = 140 and 0.4x + 0.9y = 105 on the graph to determine the value of x and y.

The equations intersect each other at (42,98). So solution of equations is x = 42 and y = 98.

So answer is,

First fruit drink = 42 pints

second fruit drink = 98 pints