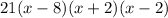We are given the following expressions
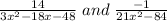
We are asked to find the least common denominator (LCD) for the above expressions.
First of all, we need to factor out both the denominators
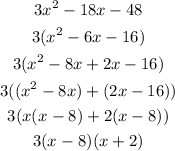
Similarly, factor out the other denominator
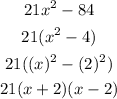
So, the expressions become
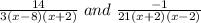
The least common denominator (LCD) is